Leetcode #21 Merge Two Sorted List

You are given the heads of two sorted linked lists list1 and list2.

Merge the two lists in a one sorted list. The list should be made by splicing together the nodes of the first two lists.

Return the head of the merged linked list.

 

Example 1:

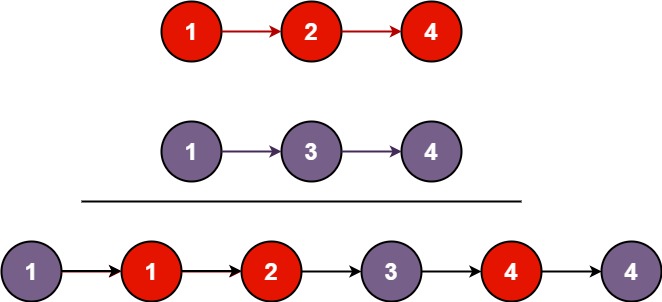
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

Example 2:

Input: list1 = [], list2 = []
Output: []

Example 3:

Input: list1 = [], list2 = [0]
Output: [0]

 

Constraints:

• The number of nodes in both lists is in the range [0, 50].
• -100 <= Node.val <= 100
• Both list1 and list2 are sorted in non-decreasing order.

Idea Behind the solution

• Maintain a head on the merged linked list.

• Then choose the head of the merged linked list by comparing the first node of both linked lists.

• For all subsequent nodes in both lists, you choose the smaller current node and link it to the tail of the merged list, and moving the current pointer of that list one step forward.

• You keep doing this while there are some remaining elements in both the lists.

• If there are still some elements in only one of the lists, you link this remaining list to the tail of the merged list.

Solution

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if (list1 == nullptr) { return list2; }
        if (list2 == nullptr) { return list1; }

        ListNode* head = nullptr;
        if (list1->val <= list2->val)
        {
            head = list1;
            list1 = list1->next;
        } else {
            head = list2;
            list2 = list2->next;
        }
        ListNode* current = head;
        while (list1 != nullptr && list2 != nullptr) {
            if (list1->val <= list2->val)
            {
                current->next = list1;
                list1 = list1->next;
            } else {
                current->next = list2;
                list2 = list2->next;
            }
            current = current->next;
        }

        if (list1 == nullptr) { current->next = list2; }
        if (list2 == nullptr) { current->next = list1; }
        
        return head;
    }

};  

Time Complexity 

We will finally traverse each list only once in these two loops so time complexity will be O(m+n) if m and n denotes to amount of nodes of these two lists.

m is the length of the first list's size.

n is the length of the second list's size. 

In the worst case, It has to traverse through the entire two lists, so it is O(m+n).

Space Complexity

It’s trivial that it only uses O(1) extra space.

The space complexity of the algorithm is O(1) because we only use a constant amount of extra space regardless of the size of the input lists.

Reference 

LC link