Edit Distance (#72 Leetcode)

 Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

• Insert a character
• Delete a character
• Replace a character

 

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

 

Constraints:

• 0 <= word1.length, word2.length <= 500
• word1 and word2 consist of lowercase English letters.

Algorithm Explanation

Recursive Formula 

class Solution {
public:
    int minDistance(string text1, string text2) {
        short m = text1.size(), n = text2.size();
        short dp[m+1][n+1];
        for (int i = 0; i <= m; i++) {
           dp[i][0] = i;
        }
        for (int i = 0; i <= n; i++) {
           dp[0][i] = i;
        }
        /*for (int i = 0; i < m+1; i++) {
            for (int j = 0; j < n+1; j++) {
                cout << dp[i][j] << " ";
            }
            cout << "\n";
        } */
        
        for (int i = 1; i <= m; i++) {
           for (int j = 1; j <= n; j++) {
              dp[i][j] = (text1[i-1] == text2[j-1]) ? (dp[i-1][j-1]) : (min(dp[i-1][j], min(dp[i][j-1], dp[i-1][j-1])) + 1);
              
           }
        }

       /* for (int i = 0; i < m+1; i++) {
            for (int j = 0; j < n+1; j++) {
                cout << dp[i][j] << " ";
            }
            cout << "\n";
        }*/
        return dp[m][n];
    }
};

Program Explanation 

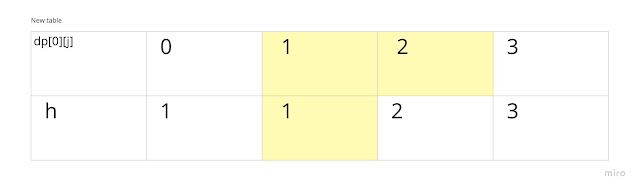
When the text1[i] not matches with text2[j], it will get the minimum of among the below three which are depicted in yellow.

1. dp[i-1][j]

2. dp[i][j-1]

3. dp[i-1][j-1]

The minimum is 1 from the above three cells and add 1 to it. So, the value of dp[i][j] would be 2 when i is 1, and j is 2

The cells highlighted in light green are when the character matches. The last cell would be the return value of the edit distance function. 

Considering the worst case scenario, 0th row and 0th column will be initialised. 

Time Complexity is O(n.m)

References

https://www.youtube.com/watch?v=XYi2-LPrwm4