Design & Analysis of Algorithm

Hey all, 

I prepared this for one of the career awareness program conducted in my college. For the first half-an-hour, I explained how the DAA is useful in my career, and later for the last few minutes, I was going through this post. Let's get into this vast topic. 

Usually a program requires a number of resources:

1. Memory 
2. I/O
3. Processing 
4. Disk 

Every line of a code is written at the cost to the system. The cost depicts the resources it uses which could be: 

• CPU cycles 
• Memory 
• Network 

We are more concerned about CPU cycles ie., time and memory. Every operation in the logic takes time. These operations could be an assignment, read operation, conditional, loop, etc., It is fair to compare and measure these algorithm with its number of operations. 

Why Data Structures are needed? 

Though memory is available to store all the data, retrieving and accessing the user's data will be as fast as possible if data structures are used. 

Will cover this in another post in future. 

How the retrieving & accessing would be faster?

Accessing and retrieving the data would be faster if an algorithm/program is efficient.  

Algorithm 

• Algorithm is a function/program in my perspective. 
• A sequence of steps/operation is to be carried out in order to solve a specific computational problem. 
• Algorithm is a plan for solving a problem.

Algorithm expresses the high level idea to solve a problem, and this idea doesn't depend on the choice of the programming language or the architecture of the underlying machine.Thus algorithm design is not concerned with these "little details". In a sense, an algorithm is what left unchanged when you translate from one programming language to another. 

In principle, an algorithm being just an idea, can be expressed in any way. It can also be expressed in plain English but it lacks precision. To express our ideas clearly we use pseudocode. 

If a same user tries to connect to the residential gateway again, it should be discarded. How we can solve this problem? Writing an algorithm(solution) would solve this problem, but if the users are more, we are in need of an effective & optimized algorithm. 

Eg:

struct clients { int id; char ip_addr[32]; char name[20]; }; struct clients *usr_list; void reg_accept_users(struct *usr_list, int num_users, int user_id) { int i; for (i = 0; i < num_users; i++) { if (user_id == usr_list.id[i]) { printf(" User Name %s is already connected\n", usr_list.name[i]); break; } } }

If a program is utilized by multiple people, It will definitely be called as algorithm. As it fulfills the purpose of others' problem, it will further be called as algorithm. 

Designing an Algorithm

Insertion Sorting 

Quick Sort

Binary Search Tree

Why we need to analyze an algorithm?

Why an algorithm design is important? (Design of Algorithm)

For a single input, the algorithm will work perfectly. To run the program faster when the input size grows, an effective algorithm is required, and also CPU work should be reduced. Also, an inefficient algorithm would be slow for the system to be usable.

Why we need faster algorithm?

Faster algorithm is needed to save money & time, so measuring an algorithm's performance is very much important. 

Often, these algorithms are non-trivial, and it is not clear why they perform the tasks clearly. If you do feel so, welcome to the world of Algorithms ;-)

Algorithm design is not programming tricks. Optimising a program doesn't fall under algorithm design rather focusing on scalability of the algorithm.

Why we need to analyse an algorithm? (Analysis of Algorithm)

Algorithm analysis is required for their correctness and efficiency. There are a few different criteria against which we can measure the efficiency of algorithms. Most common one is Time. Occasionally we are interested in Space also. Often there is a trade off between time and space : you can save time by using more memory/space. 

Two parameters define the algorithm's usefulness or analyse the performance

• Time complexity 

            While analysing the time taken by algorithm, we are not interested in the number of seconds/minutes/hours taken. This is because it depends on various factors like speed of the CPU or the skill of the programmer. Instead, we measure the running time of an algorithm by the number of "steps" it takes. 

            If the time taken by algorithm increases with its problem size, this relation is termed as time complexity. It is a measure of how efficient a program is for large inputs. We are interested in the worst-case running time of an algorithm, Click here to know why the worst case. 

• Space complexity 

            It refers to the amount of working memory (ie., excluding the memory for storing the inputs and outputs)  used by the algorithm. If the memory used by algorithm varies with the size of the problem, this relation is termed as space complexity. It is a measure of how efficient your code is in terms of memory used. 

These two terms are for performance analysis.

Time Complexity 

Time complexity will be calculated by 'counting' the number of operations performed by the code. It is defined as a function of the input size 'n' using Big-O-notation. 

n indicates the input size, while O is the worst-case scenario growth rate function. Big-O-notation is used to classify the algorithms based on their running time or space as the input grows. 

O(f(n))

T(n) = O (f(n)) where n is infinity

For example, 

f(n) = {2n^2 + n ^3 + n + 1}

If c & n are constants,

T(n) = O(Cn^2 + n^3 + n + C) would result

T(n) = n^2                        

Highlights about Big O Notation

Big O notation is a framework to analyze and compare algorithms. 

The amount of work CPU has to do (Time Complexity) as the input size grows/scales. 

Big O = Big Order function. Drop constants and lower order terms. Eg: O(3*n2 + 10n + 10)  becomes O(n2)

Big O notation cares about the worst scenario. 

Sequential Statements 

Statements with basic operations like comparisons, assignments, and reading a variable take constant time each O(1). We can also say all primitive operations like 'multiplication', 'subtraction', 'division', 'modulo', 'bit shift', etc., have a constant runtime. 

Total time complexity would be: 

Total = time(statement1) + time(statement2) + time(statement3)

If each statement executes a basic operation, it takes constant operation O(1). 

T(n) = t(statement1) + t(statement2) + t(statement3)                                 

T(n) = O(1) + O(1) + O(1) + ......

As time complexity is calculated based on the worst case scenario, time complexity for the above lines of program is O(1). 

You might ask me why the time complexity is O(1) instead of the sum. We need to consider only the worst case, but here everything is a constant time. So, it is O(1).

Not all the statement translates to constant time, so if there is any function, we need to calculate the Big-O for each statements in the function. 

Conditional Statements 

Conditional Statements like 'if condition' take time based on the complexity in either of these condition. 

void list_append(list_t **list_head, int num)
{
    list_t *temp, *iterator;
    
    temp = (list_t *)malloc(sizeof(list_t));
    temp->data = num;
    temp->next = NULL;

    if (*list_head == NULL) {
        // If list is empty
        *list_head = temp;
        //printf("%s %d %d\n",__func__,__LINE__,(*list_head)->data);
    } else { 
        iterator = *list_head;
        while (iterator->next != NULL) {
             iterator = iterator->next;
        }
        iterator->next = temp;
        //printf("%s %d %d\n",__func__,__LINE__,temp->data);
    }

    return; 
}

Total time complexity would be either of these condition but not both.  

Total = time(statement1) in if condition 

Total = time(statement1) + time(statement2) + time(statement3)  in else condition 

T(n) = Complexity of if/else condition

Loop Statements 

The number of statements the loop is iterated the complexity is folded to that number of times. Loop Statements like 'if condition' take time based on the complexity in either of these condition. 

for (i = 0; i < n; i++) 
{
   /* Statement 1's complexity is O(1) */
   /* Statement 2's complexity is O(1) */
   /* Statement 3's complexity is O(1) */
}

The total complexity of logic within for loop is O(1+1+1) = O(3)

Unfolding the loop, it runs 'n' number of times. Hence, n increases the number of statements increasing proportionally increasing the complexity. Since, it is directly proportional to 'n' and each i-th iteration, complexity is O(3), hence now the total complexity becomes

O (3*n)

As per the Big-O notation rules, we ignore constants as the value of 'n' increases to really large value, so the complexity of a single loop has been computed as, 

O(n)                                       

Nested Loops

for (i = 0; i < n; i++) 
{
   for (j = 0; j <n; j++) {
       /* Statement 1's complexity is O(1) */
       /* Statement 2's complexity is O(1) */
       /* Statement 3's complexity is O(1) */
   }
}

For increase in 'n', the complexity would increase exponentially. If n is 2, the total number times statement 1 to 3 will be executed is 4. If 'n' is 3, it will be executed 9 times. 

So, the time complexity for the nested loop is O(n*n)

     O (n^2)                                   

To be updated.......

The common data structures' operations

There are eight time complexities 

Yes constant time i.e. O(1) is better than linear time O(n) because the former is not depending on the input-size of the problem. The order is O(1) > O (logn) > O (n) > O (nlogn).

Constant Time O(1)

Have already explained more about constant time for O(1). 

Logarithmic Time O(log n)

This applies to the algorithms which divides the problem in half every time. Eg: Binary Search

For instance, if we need to find a word in the dictionary, what are the methods available? 

Algorithm A 

Search each word by word from the beginning. 

for (i = 0; i < n; i++) {
   if (a[i] == search_element) {
       return a[i]; 
   }
}

Algorithm B

1. Go to the middle of the dictionary and check the first word on it. 

2. If the word to be searched is greater than this, go right. 

3. If the word to be searched is less than this, go left. 

4. If the word to be searched is found, return it.

5. After going right, get the middle from right till the end. Repeat from step 1. 

6. After going left, get the middle from left till the start. Repeat from step 2.

/* Search the node and its parent value */ // Logarithmic Time O(log n) int search_node(tree_t *root, int num, tree_t **parent) // { // int result = 0; // 1 => O(1) // if (num == root->data) { // return 1; // 1 => O(1) } else { // *parent = root; // 1 => O(1) if (num < root->data) { // search_node(root->left, num, parent); // n^(log b a) + log n } else { // result = search_node(root->right, num, parent);// n^(log b a) + log n } } return result; }

The complete tutorial of Binary Search Tree implementation is available here. 

Finding the runtime of recursive algorithm 

• T is the Time Complexity 
• n is the input array size 
• a is the number of sub-problems. For our case, we only split the problem into one subproblem. So, a = 1. Precisely, either one of the condition is recursively called. 
• b is the factor by which n is reduced. For our example, we divide the n in half each time, so we need to compare max of half of the elements which makes the complexity as O(log n).
• f(n) is the running time outside the recursion. Since dividing by 2 is constant, we have f(n) = O(1).                                         

                             is for the recursive function 

                                       is for dividing array size by half. (log is to the base of 2)

      Master method formula    T(n) = a T (n/b) + f(n)

      In this example, we would get 1 as run-time for the recursive algorithm.  

    As we need to concentrate on the worst case scenario, we need to care both recursion and outside recursion runtime. 

    So, it would be  

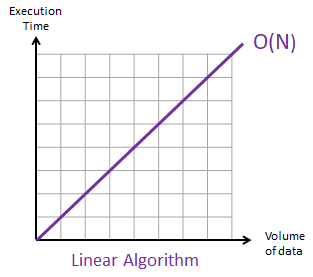
If we resolve O(n ^ log b a), it will result O(1 log (n)). O(log n) is the runtime for binary search. Recursion & for loop will affect the runtime of the code.  

Linear Time O(n)

int get_min_list (list_t *list_c) // Linear Time O(n) { // if n is 3 | If n is 5 | if n is 10 int count = 0; // 1 | 1 | 1 int min = 0; // | | while(list_c != NULL) { // 1 | 1 | 1 ***************************** // | | if (list_c->data < min) { // 2(n) | 5(n) | 10(n) min = list_c->data; // | | } // | | ***************************** // | | } // | | return count; // 1 | 1 | 1 }

If the input size (n) is 3, f(n) would be

f(n) = 1 + 1 + 2(n) + 1  

Now, we need to ignore the constants and lower order terms. 

This means if the input array size grows, the time taken to compute this algorithm is proportional to the input array size. Why can't it be O(1) ?  We always care about the worst case. 

Examples of Linear Time Algorithms 

• Get the min/max in an array 
• Print all the elements in the array 
• Find a given element in a collection - This might lead a O(1) as well if the element is found at first. 

Quadratic Time O(n^2)

Already covered this is nested loop above. 

Space Complexity

For any program, memory may be used for the following:

1. Variables (Data Space)

    Data Space is the amount of space used by the variables and constants. 

2. Execution (Environmental Stack)

    Sometimes an algorithm(function) may be called inside another algorithm(function). In such a situation, the current variables are  pushed onto the system stack, where they wait for further execution and then the call to the inside algorithm(function) is made. 

For example, If a function A() calls function B() inside it, then all the variables of the function A() will get stored on the system stack temporarily. while the function B() is called and executed inside the function A(). 

3. Program Instruction (Instruction Space)

    Instruction Space is the amount of memory used to save the compiled version of instructions. 

But while calculating the Space complexity of any algorithm, we usually consider only Data Space and we neglect the Instruction Space and Environmental Stack. 

We need to consider the below two parameters to calculate the space complexity. 

1. Constants (independent)
2. Variables (dependent)

        S(P) = C + S                                

Here, C denotes constants and S denotes variable.

Eg 1 - Constant Space Complexity

int add( int a, int b, int c) 
{

    int Z;

    z = a + b + c;
    return z;
}

In the above example, integer takes 4 bytes of memory, and this space requirement is fixed. Hence it is called Constant Space Complexity.  

Eg 2 - Linear Space Complexity

void add( int a[], int n) 
{
    int x; 
    for (i=0; i<n; i++) {
       x = x + a[i];
    }
    return x;
}

• In the above code, 4*n bytes required for the array a[] elements. 
• 4 bytes are required for x, n, and i. 

Hence the total memory requirement will be (4n + 12), which is increasing linearly with the increase in the input value n. Hence it is called Linear Space Complexity. 

Space complexity should be maintained minimum for any algorithm. 

Additional space/memory is measured in terms of the largest memory use by the program when it runs. 

If O(N) memory is allocated, and later free it, that does not make the space complexity of program O(1).

Reference: Adrianmejia, go4expert, interviewbit, studytonight