Binary Search Tree (BST)

Tree is any graph that doesn't have cycle. 

Difference between Binary Tree and Binary Search Tree

  1. Binary tree is the tree in which every node has no, one or utmost two children. There is no condition or relationship between the values of the parent and children nodes.
  2. But in binary search tree (which also inherits the properties of a binary tree), the node with value smaller than the parent node must become the left child and the node with value greater than or equal to the parent node must become the right child.
  3. Which is why, in a normal binary tree you cannot say anything about a random node. Where as in a binary search tree, given a random node (that exists in the tree), I can say that it is either in the left subtree or right subtree with respect to a parent node.
  4. Also, inorder traversal of a binary search tree results in sorting of the tree elements.
  5. An element in a binary search tree call be searched in O(log n) to the base 2 complexity but you cannot promise this in a normal binary tree.

This post covers the following:
1. Insert node based on sorting
2. Inorder
3. Preorder
4. Postorder
5. Search the node and its parent value
6. Properties of the BST 

Note: Duplicates in binary tree are not allowed, but we can have a count variable in the structure to count the number of entries repeated.

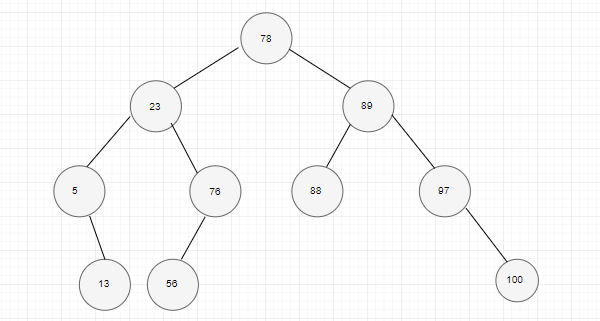
/*                        78 
 *            23                    89
 *    5               76        88        97
 *        13      56                           100
 */

#include <stdio.h>
#include <string.h>
#define NUM_OF_NODES 10
#define MORE_CPU_CYCLING 1

typedef struct tree_n {
   int data;
   struct tree_n *left;
   struct tree_n *right;
} tree_t;

tree_t *create_node(int num)
{
   tree_t *node = (tree_t *)malloc(sizeof(tree_t));
   node->data = num;
   node->left = NULL;
   node->right = NULL;
   return node;
}

/* Search the node and its parent value */
int search_node(tree_t *root, int num, tree_t **parent)
{
   int result = 0;
   
   if (num == root->data) {
       return 1;
   } else {
       *parent = root;
       if (num < root->data) {
           search_node(root->left, num, parent);           
       } else {
           result = search_node(root->right, num, parent);           
       }
   }       
   return result;
}

/* Left - Right - Root */
void postorder(tree_t *node) 
{
    tree_t *parent = NULL;
    if (node == NULL) {
        return;
    }

    postorder(node->left);
    postorder(node->right);
    printf("%d ", node->data);
}

/* Root - Left - Right */
void preorder(tree_t *node) 
{
    tree_t *parent = NULL;
    if (node == NULL) {
        return;
    }

    printf("%d ", node->data);
    preorder(node->left);
    preorder(node->right);
}

/* Left - Root - Right */
void inorder(tree_t *node) 
{
    tree_t *parent = NULL;
    if (node == NULL) {
        return;
    }

    inorder(node->left);
    printf("%d ", node->data);
    inorder(node->right);
}

/* Insert the node by sorting */
void insert(tree_t **root, int num)
{
   
   if (*root == NULL) {
       tree_t *node = create_node(num);
       *root = node;
   } else {
       if (num < (*root)->data) {
           insert(&((*root)->left), num);
       } else {
           insert(&((*root)->right), num);
       }
   } 
   return;
}

int main ()
{
   tree_t *root = NULL, *parent = NULL;
   int iterator = 0, found = 0;
   int a[] = {78, 23, 76, 56, 5, 13, 89, 88, 97, 100};
#ifdef MORE_CPU_CYCLING
   while (iterator < NUM_OF_NODES) {
       insert(&root, a[iterator++]);
   }
#else
   // Do nothing
#endif
   printf("Inorder:");
   inorder(root);
   printf("\nPreorder:");
   preorder(root);
   printf("\nPostorder:");
   postorder(root);

   found = search_node(root, a[NUM_OF_NODES-1], &parent);
   if (found) {
       printf("\nThe searched number %d is found, and its parent is %d", 
              a[NUM_OF_NODES-1], parent->data);
   } else {
       printf("\nThe searched number is not found");
   }
   return 0;
}

Output:
1
2
3
4

Inorder:5 13 23 56 76 78 88 89 97 100 
Preorder:78 23 5 13 76 56 89 88 97 100 
Postorder:13 5 56 76 23 88 100 97 89 78 
The searched number 100 is found, and its parent is 97

<Delete to be updated >

Property of the BST 

  • All the data which is larger will be placed at the right-hand side of the node. and similarly, the data with less value will be placed at the left-hand side of the node.  
  • The position of the root node can't be changed. 
  • The root node is fixed, and the root node of the subtree is also fixed. 
  • If the nodes lie in the same path towards the root node, the nodes can't be exchanged. In other words, the root of the subtree is fixed. 
  • Nodes on the left and right subtree can be in any order. The ordering between them left and right subtree is irrelevant as they are independant. 

Valid- Permutation in BST

A valid permutation is obtaining the same BST by changing the position of the node. 

Let's try to find the total number of valid permutations for the given array. 

Eg: Original tree
   int a[] = {78, 23, 76, 56, 5, 13, 89, 88, 97, 100};



If the root node's subtree position is changed, the array would be:

   int a[] = {78, 23, 76, 56, 5, 13, 88, 89, 97, 100};




This leads to an invalid permutation, and this can't be taken into account. This confirms the root of the subtree can't be changed.

   int a[] = {78, 23, 76, 56, 5, 13, 100, 89, 97, 88};



The above doesn't provide the original BST.  If the nodes lie in the same path towards the root node, the nodes can't be exchanged. 

The array will have any of the following permutation:

   int a[] = {78, 23, 76, 56, 5, 13, 89, 88, 97, 100};

   int a[] = {78, 23, 76, 56, 5, 13, 89, 97, 88, 100};

   int a[] = {78, 23, 76, 56, 5, 13, 89, 97, 100, 88};



This ensures the nodes on the left and right subtree can be in any order in the array, but left nodes or right nodes will not be mixed together. The ordering between the left hand side is strict, similarly on the rght hand side. 

For example, 

   int a[] = {78, 23, 76, 56, 5, 13, 89, 100, 97, 88};

This led to invalid permutation. 

Combinatorics 

The number of valid combination of any node is the number of left children multiplied by the number of right children with m + n C m

valid combination of a single node is 1, and the valid combination of an empty node is also 1. 

This is related to a recursive data structure. The best example of recursive data structure is Linked list. 

Reference: Gaurav Sen Youtube Video 


Comments

Post a Comment