Find Eventual Safe State (#802 Leetcode)

There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].

A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node.

Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.

 

Example 1:

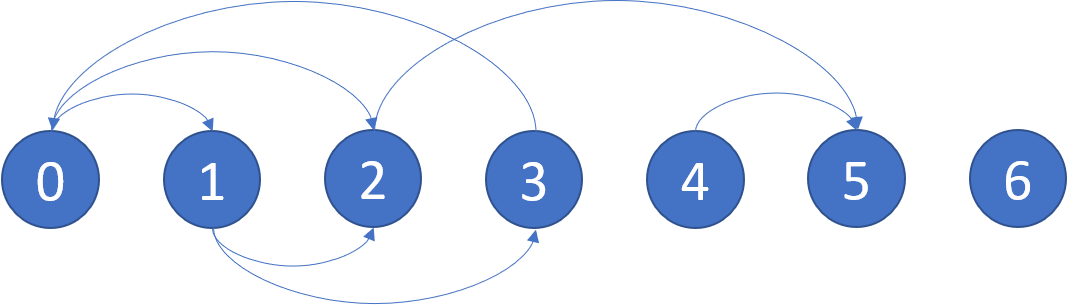
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

Each graph[i] contains the edges of the node in graph[i]. 

In example 1, 

Path 1:

From 0th vertex, there are two edges [1, 2]. As we are going to traverse in DFS, let's take edge 1. From vertex 1, there are two edges [2, 3]. Similarly, we are taking first edge which is 2. From vertex 2, we are taking edge 5 and vertex 5, doesn't have any edges. so it gets terminated. 

Hence, vertex 5 and 2 are marked as safe node. 

Path 2 : 

If we consider the path 0->1->3->0, it will form a cycle but not lead to terminal node. Hence, 0, 1, and 3 are not safe node. 

From 0th vertex, there are two edges [1, 2]. As we are going to traverse in DFS, let's take edge 1. From vertex 1, there are two edges [2, 3]. We are  going to taking second edge which is 3 because first edge is already visited. From vertex 3, it leads to already visited vertex/node which is 0. This means it is forming a circle. Hence 3 is not a safe node. Also, 3's parent 0 is also not a safe node. 

Path 3: But, if we consider other path 0->2->5, it will lead to terminal node. So, 2 is a safe node. 

Path 4:

Similarly, the path from 4 to 5 is safe node as 4 leads only to 5. So, all the neighbours of 4 is safest. 

Path 6:

As 6 doesn't have any edge, it is going to be a safe node. 

Example 2:

Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

From this example  [[1, 2, 3, 4], [1, 2], [3, 4], [0, 4], []]

Path 1:

From 0th vertex, there are four edges [1, 2, 3, 4]. As we are going to traverse in DFS, let's take edge 1. From vertex 1, vertex 1 is marked as visited node, and there are two edges [1, 2]. Similarly, we are taking first edge which is 1.  At this point, vertex 1 is already visited, so this creates a cycle. So, vertex 1 is marked as cycle node and vertex 0 which is parent of vertex 1 also marked as cycle node. So, both nodes are not safe node. 

Path 2 : 

Let's take path from vertex 2 which has two edges [3, 4]. Considering DFS, edge 3 is taken. Vertex 3 has two edges [0, 4]. As 0 is visited already, it forms a cycle. This means vertex 2 parent is leading to cycle. So, both nodes 2 and 3 are not safe node.

Path 3: As there are no outgoing edges from vertex 4, it is a safe node. 

Constraints:

• n == graph.length
• 1 <= n <= 104
• 0 <= graph[i].length <= n
• 0 <= graph[i][j] <= n - 1
• graph[i] is sorted in a strictly increasing order.
• The graph may contain self-loops.
• The number of edges in the graph will be in the range [1, 4 * 104].

 

We can do this in O(E+V) complexity because we will not visit the node or edges which are visited already.

Note that recursion function should be invoked only for the non-visited nodes or non-explored nodes. 

class Solution {
    private:
    bool detectCycle(vector<vector<int>>& graph,
                     vector<int>& state, int node) {

	state[node] = 1;

	for (auto& adjnode : graph[node]) {
            //cout << "Node has edges " << node << " adjnode " << adjnode << endl;
	    if (state[adjnode] == 0) {
		if (detectCycle(graph, state, adjnode)) {
                    //cout << "Parent Node also forms cycle " << node << " adjnode " << adjnode << endl;
		    return true;
		}
	    } else if(state[adjnode] != 2) {
                //cout << "Child node " << adjnode << " of parent " <<  node  << " got visited already " << endl;
		return true;
	    }
            //cout << "Next edge for " << node << " adjnode " << adjnode << endl;
	}

        //cout << "Safe node " << node << endl << endl;
	state[node] = 2;
	return false;
    }
public:
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
	int n = graph.size();

	vector<int> state(n, 0);

	for (int i=0; i<n; i++) {
	   if (state[i] == 0) {    
               //cout << "Non-visited node " << i << endl;
	       detectCycle(graph, state, i);
	   }
	}

	vector<int> safeNodes;

	for (int i=0; i<n; i++) {
	    if (state[i] == 2) {
	        safeNodes.push_back(i);
	    }
	}

	return safeNodes;
    }
};